HyperLogLog - Efficient Cardinality Estimation

Prem published on December 08, 2024

5 min, 940 words

A few months ago, I came across a really cool data structure called HyperLogLog. It was super interesting to learn how it works!

Imagine, we've an array and we want to find the number of distinct elements in it.

The most straighforward approach would be to go over each element in the array and track the distinct elements using a set or a hashmap.

This is a basic algorithm with linear space and time complexities.

The Problem with Linear Algorithm

Assuming, an array of 32 bit integers on a machine capable of performing $10^8$ operations in a second.

Here is a table showing how much memory and time this algorithm would consume for different array sizes:

Array Size	Time Taken	Memory
100 million	1 second	381 MB
1 billion	10 seconds	3.72 GB
10 billion	1.67 minutes	37.25 GB
100 billion	16.67 minutes	372 GB
1 trillion	2.78 hours	3.636 TB
10 trillion	28 hours	36.36 TB

As array sizes grow, time and memory requirements increase rapidly. For instance, processing 10 trillion elements would require 36 TB of memory and 28 hours!

This is where HyperLogLog shines. It’s a probabilistic data structure that provides highly accurate estimates of distinct elements while using significantly lesser amount of memory and time.

The Underlying Concept

Vehicle Registration Number Analogy

Have you ever noticed how people go crazy for those fancy vehicle registration numbers? The transport department even does auctions for these fancy registration numbers and people spend a lot of money for it.

When people are spending their money for numbers like 0001, 4444, or 9999, they are just choosing something that stands out.

People love these because they feel unique, right? Such numbers are rare and less likely to repeat in a random set of vehicle's registration numbers.

They are rare and unique. Fine, but how can we measure how unique something is? This is where probability helps.

Let’s use binary numbers to understand this concept.

Probability of Consecutive Zero Pattern

For a 3-bit binary number, there are 8 possible combinations. Among them, the pattern 000 appears exactly once:


...000	...100
...001	...101
...010	...110
...011	...111

Mathematically:

Probability of encoutering a pattern with k consecutive zeroes is

\frac{1}{2^k}

In simpler terms, a sequence of k consecutive zeroes will occur once in every $2^k$ distinct elements, on average.

If we observe a pattern of k consecutive zeroes in a uniformly distributed dataset, it implies that the dataset likely has $2^k$ distinct elements.

Hence, by simply tracking the longest sequence of consecutive zeroes, we can estimate the number of distinct elements in a dataset.

Also, The algorithm uses a hash function to transform the original data into uniformly distributed random numbers.

With this, we’ve established the base of the algorithm.

Quick Riddle:

If all patterns in the above table have the same probability of occurence, why do we focus on consecutive zeroes for this algorithm?

Show Answer

Because, the consecutive pattern can be extended to higher number of bits easily.

Improving Accuracy

Improvement 1: Using Multiple Hash Functions

The above algorithm gives a good estimate, but it is still far from accurate.

To improve the accuracy, we can use multiple independent hash functions and record the longest sequence length for each.

Finally, we calculate the average of these values for a better estimate.

Improvement 2: Single Hash Function with Bucketing

Using multiple hash functions is computationally expensive. Instead, we can use a single hash function and divide the results into $2^b$ buckets.

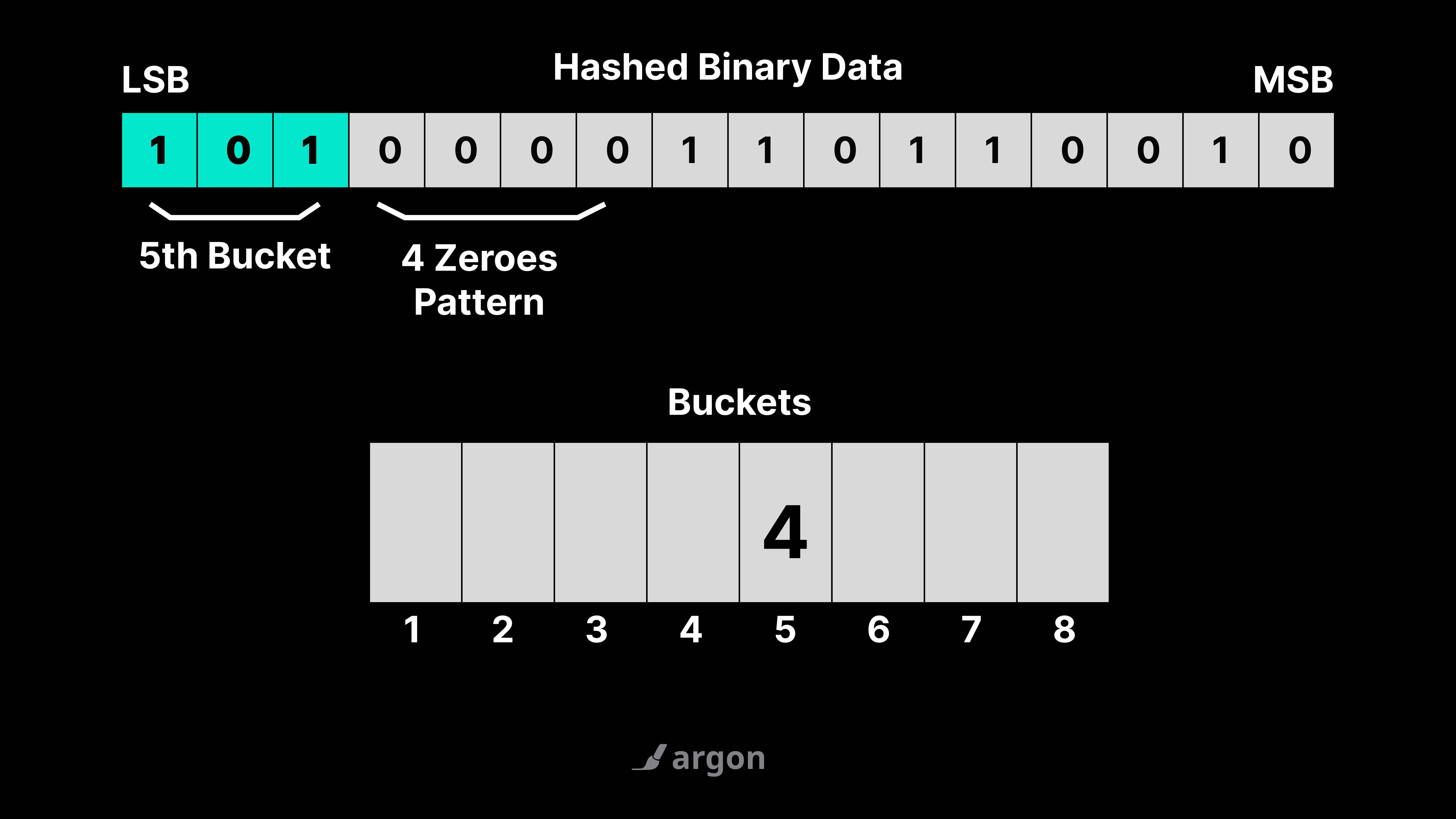
The first $b$ bits of the hash determine which bucket to use.
And the remaining bits are used to find the length of consecutive zeroes for that bucket.

And at the end, we just take the average of the maximum lengths recorded in all buckets.

Improvement 3: Harmonic Mean over Arithmetic Mean

This is an improvement in the last step, especially when we're averaging the results from different buckets.

Instead of using the arithmetic mean to merge the results from different buckets, HyperLogLog uses the harmonic mean.

Harmonic mean is better at handling outliers, which ensures more accurate results.

For example, suppose, most of our buckets have similar values except one, which is the outlier.

6,5,7,100

The Arithmetic Mean would calculate to
$=\frac{6+5+7+100}{4}=29.5$
and the Harmonic Mean would be
$=\frac{4}{\frac{1}{6} + \frac{1}{5} + \frac{1}{7} + \frac{1}{100}}\approx7.69$

We can see, the harmonic mean provides a better result by minimizing the effect of the outlier.

For a basic implementation of the HyperLogLog algorithm, visit my GitHub repository here: argon17/HyperLogLog